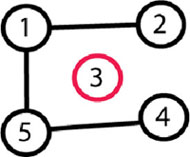
Энэ тодорхой ойлгомжтой дасгал байсан, алдах хүн байхгүй байлгүй.
int main() {
string a;
cin >> a;
for (int i = 0; i < (int)a.size(); ++i) {
if (string("CAMBRIDGE").find(a[i]) == string::npos) {
cout << a[i];
}
}
cout << endl;
}
B:
Эхлээд мэдэгдэж байгаа дүнгүүдээ буурахаар эрэмбэлье. Одоо дээрээс нь эхлэн оролцогч бүр дээр түрүүлэх боломжтой эсэхийг нь шалгая, К дугаар оролцогч гэж үзье. Энэ оролцогч түрүүлэхийн тулд бусад оролцогчидод хэдэн оноо өгөх вэ л гэсэн бодлого юм. Дараах Greedy санааг ашиглана. К дугаар оролцогчоо түрүүлүүлэхийн тулд шууд N оноог өгөх нь ойлгомжтой. Буурахаар эрэмбэлсэн учир К-н доор байгаа хүмүүс бидэнд огт хамаагүй, тэд нарт хэдэн ч оноо нэмээд К дугаар оролцогчийн дээр гарч чадахгүй. Харин К-н дээр байранд байгаа хүмүүсийг К-н дээр байлгахгүй тулд аль болох хамгийн бага оноог өгөх ёстой. Дахиад сайн бодъё, К-н дээр байгаа хамгийн өндөр оноотой тамирчинд 1 оноог өгнө, хамгийн өндөр оноотой 2 дахь тамирчинд 2 оноо гэх мэтчилэн К-1 дахь тамирчинд К-1 оноо өгнө. Тэгвэл уг К дугаар тамирчин түрүүлэх зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь:
a[K] + N ≥ max{ a[1] + 1, a[2] + 2, …, a[K - 1] + K - 1 }, энд а[] массивт оролцогчидын оноог буурахаар эрэмбэлсэн байгаа.
Одоо гол асуудал нь К-н өмнөх оролцогчидын хамгийн их оноотойг яаж олох вэ? Үүнийг жижигхээн DP ашиглаад шийдчиж болно, үүнийг уншигч таньд нээлттэй үлдээе.
Бодолт: O(NlogN)
#include <cstdio>
#include <cstdlib>
#include <algorithm>
using namespace std;
int a[300000];
bool cmp(int x, int y) { return x > y; }
int main () {
int n;
scanf("%d", &n);
for (int i = 0; i < n; ++i)
scanf("%d", a+i);
sort(a, a+n, cmp);
int s = 0;
int maX = 0;
for (int i = 0; i < n; ++i) {
s += (a[i] + n >= maX);
maX = max(maX, a[i] + i + 1);
}
printf("%d\n", s);
system("pause");
return 0;
}
C:
Өгөгдсөн N тооны length(N) = (N, K, ... ) гэсэн тоонуудаас бүтсэн байг. Хэрвээ сайн бодож үзсэн бол яг К буюу өөрийг нь хуваадаггүй хамгийн бага тоо, хэдий N<=10^17 ч маш бага тоо байгаа. Миний бодлогоны хувьд 50-аас хэтрэхгүй, гэхдээ Хонгор 41 гэж аваад давуулсан байна лээ, хангалттайлдаа уг нь кк (энийг яаж шалгах вэ?? бодож үзээрэй). Одоо тэгвэл бодлого маань ерөөсөө ийм, тэр К гэдэг тоо [A ; B] завсар дахь хэдэн тооны length()-т яг тэр байгаа байрлалдаа орох вэ? Тийм тоонууд маань бүгд Length(N) = Length(K)+1 нь ойлгомжтой.
К-г багтаасан тоонуудыг яаж тоолох вэ?
[A ; B] завсарт орших өөрийг нь хуваадаггүй хамгийн бага тоог К гэе (энд яг дээрхтэй адилхан К тоог ярьж байгаа шүү), тэгвэл К-аас бага бүх тоонууд тухайг тоог хуваана гэсэн үг. Энэ нь LCM - Хамгийн бага ерөнхий хуваагдагч, LCM(1, 2, 3, ..., K-1) мөн тухайн тоог хуваана гэсэн үг. Нэмэлт шаардлага бол тухайн тоо К-д хуваагдахгүй байг ёстой. Энэ хоёр нөхцөлийг хангах тоонуудыг тоолоод L гэе. Тэгвэл бодлогын хариу Нийлбэр{ (length(K)+1)*L } энд K = 2..41 байхад хангалттай.
Одоо тэдгээр тоонуудыг яаж тоолох талаар хальт санаа өгье. [A;B] завсар дахь тоонуудаас LCM(1, 2, 3, .., K-1)-т хуваагддаг тоонуудыг тоолсон гэж үзье. Эдгээр тоонуудаас К-д хуваагддагийг хасна, мөн огтлол буюу К болон LCM(1, 2, 3, ..., K-1)-т хуваагддагийг хасах ёстой, энэ чинь юу гэсэн үг вэ гэхээр LCM(1, 2, 3, ..., K)-г олоод хасчина гэсэн үг. Ерөнхийдөө бол А болон В-д харьяалагдах D-д хуваагддаг тоог тоолох ба дараах томёо хүчинтэй: B / D - (A - 1) / D, Үүнийг яагаад гэдэгийг өөрсдөө оролдож хараарай, уг нь энгийн л зүйллдээ.
#include <iostream>
#include <vector>
using namespace std;
int main(){
long long A, B, ret = 0;
cin >> A >> B;
// LCM = lcm(1, 2, ..., K-1)
long long LCM = 1;
int length[42];
length[2] = 1;
for (int K = 2; K < 42; K++){
for (int i = 2; i < K; i++) {
if (K % i != 0) {
length[K] = length[i] + 1;
break;
}
}
long long tempLCM = LCM;
vector<int> lcmNumbers;
for (int p = 2, k = K; k > 1; p++) {
if (k % p == 0) {
lcmNumbers.push_back(p);
while (k % p == 0) {
k /= p;
}
}
}
if ((int)lcmNumbers.size() == 1) {
tempLCM *= lcmNumbers[0];
}
ret += (length[K] + 1) * (B/LCM - (A-1)/LCM);
if (tempLCM > B || tempLCM < 0) break;
ret -= (length[K] + 1) * (B/tempLCM - (A-1)/tempLCM);
LCM = tempLCM;
}
cout << ret << endl;
}
D болон E::
Энэ хоёрын бодолт бол хоюулаа тодорхой шууд л Bruteforce хийгээд тоол, харийн өөрсдийн чинь код бичих чадвараас л шалтгаалж хүнд хөнгөн нь тодорхойлогдоно.
D бодолт:
int n, m;
cin >> n >> m;
int a[n];
for(int i=0; i<n; i++) cin >> a[i];
int sol = 0;
for(int i=0; i<n; i++)
for(int j=i+1; j<n; j++)
for(int k=j+1; k<n; k++)
if( a[i]+a[j]+a[k] <= m )
sol = max( sol, a[i]+a[j]+a[k] );
cout << sol << endl;
return 0;
E бодолт:
char a[505][505];
int sol[5];
int main()
{
int m, n; scanf("%d%d", &m, &n);
for(int i=0; i<5*m+1; i++) scanf("%s", a[i]);
for(int i=0; i<m; i++)
for(int j=0; j<n; j++)
{
int x = 1 + 5*i;
int y = 1 + 5*j;
int k = 0;
for(int l=0; l<4; l++)
k += (a[x+l][y] == '*');
sol[k]++;
}
for(int i=0; i<5; i++)
printf("%d%c", sol[i], i==4?'\n':' ');
}
F:
Энэ бодлогыг бодлогонд Stack эсвэл рекурс өгөгдөлийн бүтэц мөн BitMask 2-г ашиглана. Эхлээд өгөгдсөн тэмдэгт мөртөө нэвтрэлт хийгээд бүх зөв хаалтуудыг Стек-даа хийгээд ав, байрлалаар нь, тэгээд битмаскаа ашиглаад бүх боломжоор нь хариугаа гаргаж аваад эрэмблэхэд бодогдоно. Кодоо цэвэрхэн бичихгүй бол TLE авахуулах тестүүд их байгаа.
#include <iostream>
#include <string>
#include <set>
#include <vector>
#include <stack>
#define FORC(it, C) for(__typeof((C).begin()) it = (C).begin(); it != (C).end(); ++it)
int main(void) {
std::string ss;
std::cin >> ss;
int n = ss.size();
std::vector< int > pos(n, -1);
std::stack< int > current;
int numOfBar = 0;
for (int i = 0; i < n; ++i) {
if (ss[i] == '(') {
pos[i] = numOfBar++;
current.push(pos[i]);
}
if (ss[i] == ')') {
pos[i] = current.top();
current.pop();
}
}
std::set< std::string > ret;
for (int i = 1; i < (1<<numOfBar); ++i) {
std::string temp ;
for (int j = 0; j < n; ++j) {
if ((ss[j] != '(' && ss[j] != ')') || !(i & (1 << pos[j]))) {
temp += ss[j];
}
}
ret.insert(temp );
}
for (auto &retOut: ret) {
std::cout << retOut << std::endl;
}
return 0;
}
Дараагийн хоёр бодлого буюу G, H хоёр дээр дахин шинэ пост зориулна. Бас С бодлого дээр би өөр маш сонирхолтой бодолт хийсэн байгаа. Тэрийгээ давхар сонирхуулнаа.
Код үлдээх уг нь муу, гэхдээ яахав сурах нэг нь сурах юм байвал сураад, сурахгүй нэг нь шууд хуулаад илгээнэ биз, надад хамаагүй асуудал.