Бодлого ойлгомжтой байх. Энэ бодлого нь Хамгийн Бага Үнэлгээт Мод буюу Minimum Spanning Tree гэх графын алгоритмуудын сонгодог бодлогуудын нэг. Мөн алгоритмыг ойлгоход болон бичихэд амархан.
Ерөнхийдөө одоогийн байдлаар Greedy санаан дээр тулгуурласан Крускалын алгоритм мөн Примын алгоритм гэх хоёр ерөнхий алгоритм байгаа. Хоорондоо бараг адилхан, гэхдээ ашиглаж байгаа өгөгдөлийн бүтцээрээ ялгаатай.
Энэ удаад Крускалын алгоритмыг тохирох өгөгдөлийн бүтэцтэй нь сонирхуулая.
Эхлээд модны тодорхойлолтоо эргэн саная. Мод гэдэг нь цикл агуулаагүй холбоост графыг хэлнэ. Хэрэв мод нь N ширхэг оройтой бол N-1 ирмэгтэй байна.
Алгоритм дараах энгийн санаан дээр тулгуурлана.
Хэрэв бидэнд N оройтой M ирмэгтэй граф өгөгдвөл N-1 ширхэг хамгийн бага оройг сонгоно. Сонгохдоо тавих шаардлага бол мэдээж сонгож байгаа оройнууд цикл үүсгэх ёсгүй. Яагаад гэвэл бид мод олж байгаа учир. Гол хүндрэл бол орж ирж байгаа оройнууд цикл үүсгэж байгаа эсэхийг хангалттай хурдан шалгах. Одоо хэрэглээ маш өндөртэй өгөгдөлийн бүтэц авч үзье
Union Find::
Union Find-г дараах бодлогон дээр тайлбарлая.
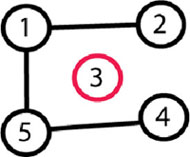
Ангид N оюутан сурдаг ба нийлдэг нийлдэгээрээ груп болон хуваагддаг. Энд транзитив чанар ажиллах ба A B хоёр найзууд, B C хоёр найзууд бол мөн A C хоёр найзууд гэсэн үг. Тэгвэл нийт оюутны тоо N <=10^6 болон хэн хэн найзууд гэдэгийг илтгэх M хос A B өгөгдсөн бол ангид хэдэн груп байгааг ол. Жишээ нь N=5 M=3, 1-2, 5-4, мөн 5-1. Тэгвэл энд дараах хоёр груп үүсэх нь:
Union Find-г үл огтлолцох ойнуудын олонлог гэж төсөөлж болно. Ой бүр нь тухайн ойг заах ганц заагчтай (санах ойн заагч биш зүгээр л тоо, гэхдээ тухайн ойд агуулагдаж байгаа хамгийн бага дугаартай модыг заагчаар сонгох болно!!!). Хоёр ойн заагч нь өөр бол энэ хоёр ой үл огтлолцох ой гэсэн үг.
Union Find-д хийгддэг үйлдэл::
х модны агуулагдаж байгаа ойн заагчийг хайж олох Find(x),
х, у гэсэн хоёр ойг нэгтгэх Merge(x, y)гэсэн хоёр л үйлдэл хийгддэг. Нэгтгэнэ гэдэг маань тус моднуудын агуулагдаж байгаа ойн заагчийг хайж олоод тухайн хоёр ойгоо ганц заагчтай болгоно гэсэн үг.
Дээрх бодлогын өгөгдсөн жишээ нь дээр нь Union Find хэрхэн ажиллахыг харья:
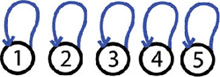
Эхлээд N=5 ширхэг ганц ганц мондоос бүрдсэн 5-н ой байгаа гэж үзье. Бүх ойнуудыг тухайн ганц модны дугаар л заана(i-р ойн заагч нь i тоо өөрөө байна).
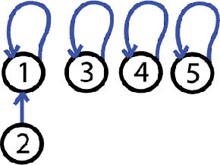
Эхний хос орж ирлээ 1-2. Энэ юу гэсэн үг вэ гэхээр 1 болон 2-р модыг агуулсан хоёр ойг нэгтэж нэг заагчтай болго гэсэн үг. Merge(1, 2):
Хоёр дахь хос орж ирлээ 4-5. Merge(4, 5);
Одоогийн байдлаар гурван груп байна.
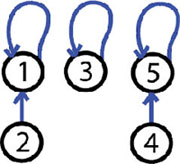
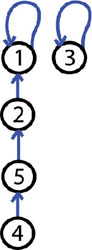
Гурав дахь хос орж ирлээ. 5-1:
Бодлогын хариу ойн тоо буюу 2.
Энэ өгөгдөлийн бүтэцийг код болгон хэрэгжүүлэхдээ дахин нэг сайжруулалт хийе. rank[i]-р i модны агуулагдаж байгаа ойн өндөрийг тэмдэглэе. Бид Union Find-аа улам хүчтэй, хурдан ажиллуулахын тулд үүсэж байгаа ойн өндөрийг аль болох бага байлгах ёстой. Жишээ нь дараах 3н ойг авч үзье:
Бид I болон J гэсэн заагчтай ойг нэгтгэхдээ аль болох ойн өндөрийг бага байлгах ёстой учраас шууд I модыг J-рүү заалгах хэрэгтэй. Жишээ нь бид I-г шууд M гэсэн модны доор аваачаад өлгөчих юм бол J гэсэн ой хамаагүй өндөр мөн хайлт хийхэд их цаг зарцуулах нь ойлгомжтой харагдаж байгаа байх. C++ дээрх код::
int parent[10001];
int rank[10001];
void createSet(int n){
for(int i=0; i<n; i++)
parent[i]=i;
}
void find(int x){
if(x!=parent[x])
parent[x] = find(parent[x]);//rekursiig butsah zamd ni tuhain mod burt ni oin zaagchiig ni onoono. Ene ni daraa dahin find hiihed barag togtmol hugatsaand hiih bolomj olgono
return parent[x];
}
void merge(int x, int y){
int px = find(x);//X modnii aguulagdaj baigaa oin zaagchiig olj bn
int py = find(y);//Y-n huvid mon adil
if(rank[px]>rank[py])parent[py]=px;//Oin ondoriig hamgiin baga bailgahiin tuld ondor oin zaagch modnoos namhan oigoo olgochihod bolno!
else parent[px]=py;
if(rank[px]==rank[py])rank[py]++;// end unendee aliniih ni ch rank-g ihegsesen bolno!
}
За одоо MST бодлогоруугаа буцаад ороё. Тэгэхээр орой бүрийг мод гэж үзээд ирмэгүүдийг орж ирэх бүрт ирмэгийн хоёр оройг нэг ойд байгаа эсэхийг шалгана. Мэдээж хоёр орой хоёр тусдаа ойд байрлаж байвал Merge хийхнээээ.
Union Find-g маш сайн анализ хийгээд өөрөө бичээрэй. Нээрээ Рекурсыг бүр сайн ашиглаж ойлгоё гэвэл хаалттай, зэрэг, үржих хуваах үйлдэл хийдэг илэрхийлэл ( 12*32/32+(32+32)*32/2 ) шууд боддог код, мөн Хоёртын хайлтын мод, Тэнцвэрт хоёртын хайлтын модыг өөрөө бичвэл тэгээд рекурс ОК гэсэн үг шүү хэхэ.
Доор MST олох C++ код тавьлаа, даалгавар болгоход MST модыг өөрийг бүх оройн хамт хэвлэнэ үү. Нэмж сонирхуулахад өгөгдсөн графын бүх ирмэгүүдийн жин ялгаатай бол MST цор ганц оршино. Энийг индукцээр баталчиж болно. Тэгвэл зарим нэг ирмэг нь ижил жинтэй бол MST хэд байж болох вэ? гээд дахиад өөр бодлого гарж ирнэ. Энэ хамаагүй хүнд бодлого болчиж байгаан. Мөн чиглэл графын хувьд бас MST олох бодлогыг дараа тайлбарланаа.
//Task: MST http://www.spoj.pl/problems/MST/
//O(E log V)
//written: Dunno
#include<cstdio>
#include<cstdlib>
#include<utility>
#include<vector>
#include<algorithm>
using namespace std;
#define edge pair<int,int>
#define Max 100001
// w(u,v)
vector< pair<int,edge> >Mst,G;
long Parent[Max];
long Rank[Max];
void MakeSet(long x){
Parent[x] = x ;
Rank[x] = 0 ;
}
long Find(long x){
if(x!=Parent[x])
Parent[x]=Find(Parent[x]);
return Parent[x];
}
void Merge(long x, long y){
long Px = Find(x);
long Py = Find(y);
if (Rank[Px]>Rank[Py])
Parent[Py]=Px;
else Parent[Px]=Py;
if(Rank[Px]==Rank[Py])++Rank[Py];
}
int main(){
//freopen("kruskali.txt","r",stdin);
//freopen("kruskalo.txt","w",stdout);
long n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)MakeSet(i);
for(int i=1; i<=m; i++){
int v,u,w;
scanf("%d%d%d",&v,&u,&w);
G.push_back(pair< int,edge >(w, edge(v,u)));
}
sort(G.begin(),G.end());
/*for(int i = 0; i<m;i++){
printf("w = %d, v = %d, u = %d\n",G[i].first,G[i].second.first,G[i].second.second);
}*/
long long res = 0LL ;
long k = 0;
for(int i=0;i<m;i++){
long Pv = Find(G[i].second.first);
long Pu = Find(G[i].second.second);
if(Pu!=Pv){
Mst.push_back(G[i]);
res += G[i].first;
Merge(Pu,Pv);
k++;
}
if(k==n-1)break;
}
printf("%lld\n",res);
return 0;}
Python дээрх код:
class DisjointSet(dict):
def add(self, item):
self[item] = item
def find(self, item):
parent = self[item]
while self[parent] != parent:
parent = self[parent]
self[item] = parent
return parent
def union(self, item1, item2):
self[item2] = self[item1]
from operator import itemgetter
def kruskal( nodes, edges ):
forest = DisjointSet()
mst = []
for n in nodes:
forest.add( n )
sz = len(nodes) - 1
for e in sorted( edges, key=itemgetter( 2 ) ):
n1, n2, _ = e
t1 = forest.find(n1)
t2 = forest.find(n2)
if t1 != t2:
mst.append(e)
sz -= 1
if sz == 0:
return mst
forest.union(t1, t2)
#test
nodes = list( "ABCDEFG" )
edges = [ ("A", "B", 7), ("A", "D", 5),
("B", "C", 8), ("B", "D", 9), ("B", "E", 7),
("C", "E", 5),
("D", "E", 15), ("D", "F", 6),
("E", "F", 8), ("E", "G", 9),
("F", "G", 11)]
print kruskal( nodes, edges )
#output: [('A', 'D', 5), ('C', 'E', 5), ('D', 'F', 6), ('A', 'B', 7), ('B', 'E', 7), ('E', 'G', 9)]
Зурагнуудыг Тодкодер болон Вики-гээс авлаа.
UPDATE:
Union Find-аар энэ бодлогыг бодно уу.
Дараагийн постууд:
- Articulation Point
- Divide and Conquer
- IOI 2011 Race бодлогын бодолт
- Bipartite Matching
- Tarjan
- Flow